| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- ROS2
- On-memory file system
- ubuntu 22.04
- Process
- SQLD
- Python
- System Call
- CNN
- Optimization
- Seoul National University
- assignment1
- Baekjoon
- Linux
- C++
- Data Science
- 밑바닥부터 시작하는 딥러닝2
- file system
- CPP
- BFS
- cs231n
- Operating System
- do it! 알고리즘 코딩테스트: c++편
- deep learning
- RNN
- Humble
- assignment2
- DFS
- Machine Learning
- Gentoo2
- computer vision
- Today
- Total
newhaneul
[Seoul National Univ: Data Science] Lecture 8. Hash Tables 본문
[Seoul National Univ: Data Science] Lecture 8. Hash Tables
뉴하늘 2025. 12. 13. 21:32본 포스팅은 서울대학교 이준석 교수님의 M2480.001100 Principles & Applications of Data Science을 수강하고 공부한 내용을 정리하기 위한 포스팅입니다.
https://youtu.be/Yb57Nqpt4D4?si=Smcb22L3ZkAKfpKo
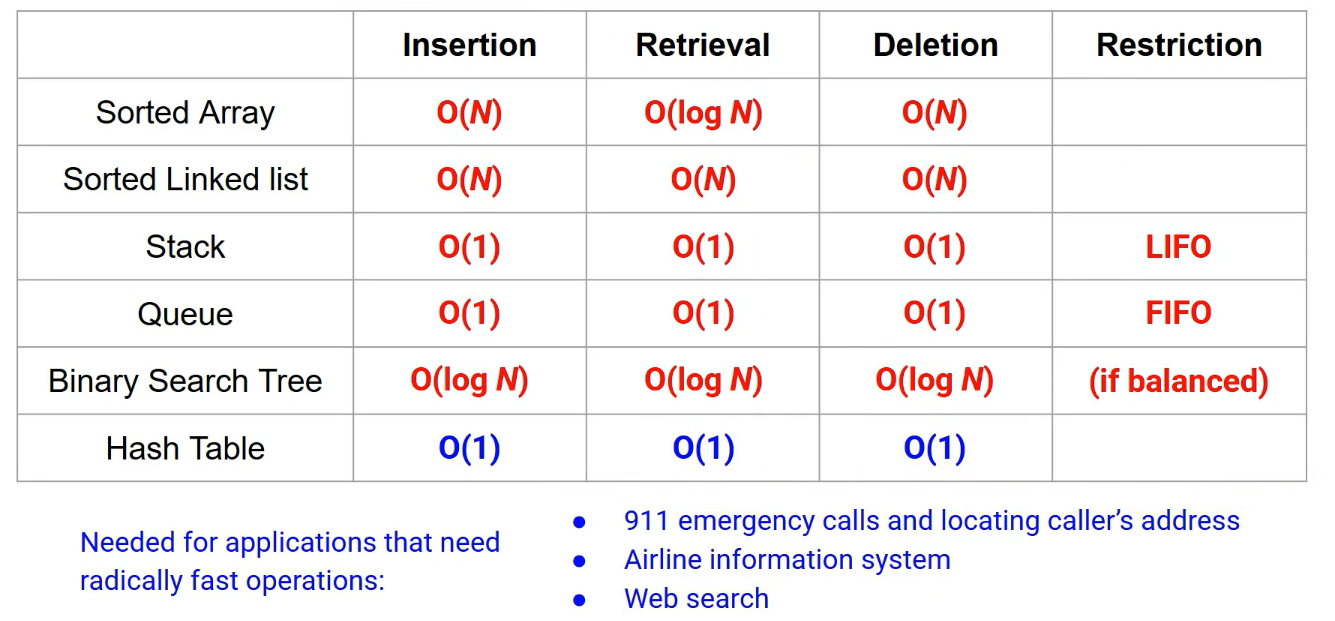
1. Data Indexed Arrays
값 자체를 인덱스로 사용해서, 그 값이 존재하는지 여부와 해당 값에 매핑된 데이터를 즉시 꺼내는 방식이다. 예를 들어 집합 [2, 5, 9, 10]을 저장할 때 일정 크기의 배열을 만들어 True/False로 표시하는 방식이다. 배열 접근 방식은 인덱스로 바로 접근하는 연산이라 삽입, 삭제, 찾기 등이 상수 시간으로 가능하다.
- Find: A[x] 한 번 읽으면 되므로 O(1)이다.
- Insert: A[x] = true 한 번 쓰면 되므로 O(1)이다.
- Delete: A[x] = false 한 번 쓰면 되므로 O(1)이다.
문제점으로는 들어올 수 있는 값의 범위가 크면 메모리 폭발 문제가 발생할 수 있다. 또한 문자열/실수 같은 비정수 키는 직접적으로 인덱스로 사용하기가 어렵다.


2. Hash Table
해시 테이블은 "Key → Address"로 빠르게 바꿔서 insertion / retrieval / deletion 연산을 O(1)에 접근하는 것을 노리는 자료구조이다. 좋은 해시 함수의 조건으로는 계산이 O(1)이어야 하고, 테이블 전체에 값이 고르게 퍼져야 한다.
아이디어
- 크기가 M인 배열을 생성한다.
- 해시 함수 h(key)가 키를 0, 1, ... M-1 범위의 인덱스로 매핑한다.
- Insertion / retrieval / deletion은 해시 값 위치로 바로 이동하므로 평균적으로 O(1)을 기대한다. 단, Collision 때문에 평균적으로 O(1)이 되는 것이고 항상 O(1)은 아니다.

Compression Functions
(1) Selection digits
- 키의 특정 자리만 뽑아서 인덱스로 사용한다.
- 단점: 키 패턴이 비슷하면 특정 자리도 비슷해서 충돌이 쉽게 발생한다.
(2) Folding
- 키를 몇 자리씩 끊어서 더한 값으로 만든다.
- 단점: 순서만 바뀐 키가 같은 합이 되어 충돌될 수 있다.
(3) Modulo arithmetic
- 가장 흔한 방식으로, 테이블 크기만큼 나눈 나머지를 인덱스로 사용한다.
테이블 크기보다 키의 종류가 더 많기 때문에, 서로 다른 키가 같은 칸으로 가는 Collision이 발생하게 된다. 따라서 이 Collision을 해결하는 방법으로 Separate chaining, Open addressing이 있다.



Open Addressing
충돌이 발생하면 다른 빈 칸을 찾아서 테이블 내부에 저장하는 방식이다. 대표적인 Probe 방식은 아래와 같다.
- Linear probing: i, i + 1, i + 2, ...
- Quadratic probing: i + 1^2, i + 2^2, ...
- Double hashing: 1 + k * h2(key)
Linear probing과 Quadratic probing은 입력은 동일하고, Collision을 어떻게 처리하는지의 방식 차이이다. 따라서 같은 입력이 계속해서 들어오면 반복하여 다른 인덱스 공간을 찾아야 하므로 비효율적이다. 이와 달리 Double hasing은 입력을 다루는 또 다른 해시 함수를 사용하기 때문에 분산 효과가 좋은 편이다.
Time Complexity는 α (load factor, N/M)이 1에 가까워질수록 급격하게 증가한다.

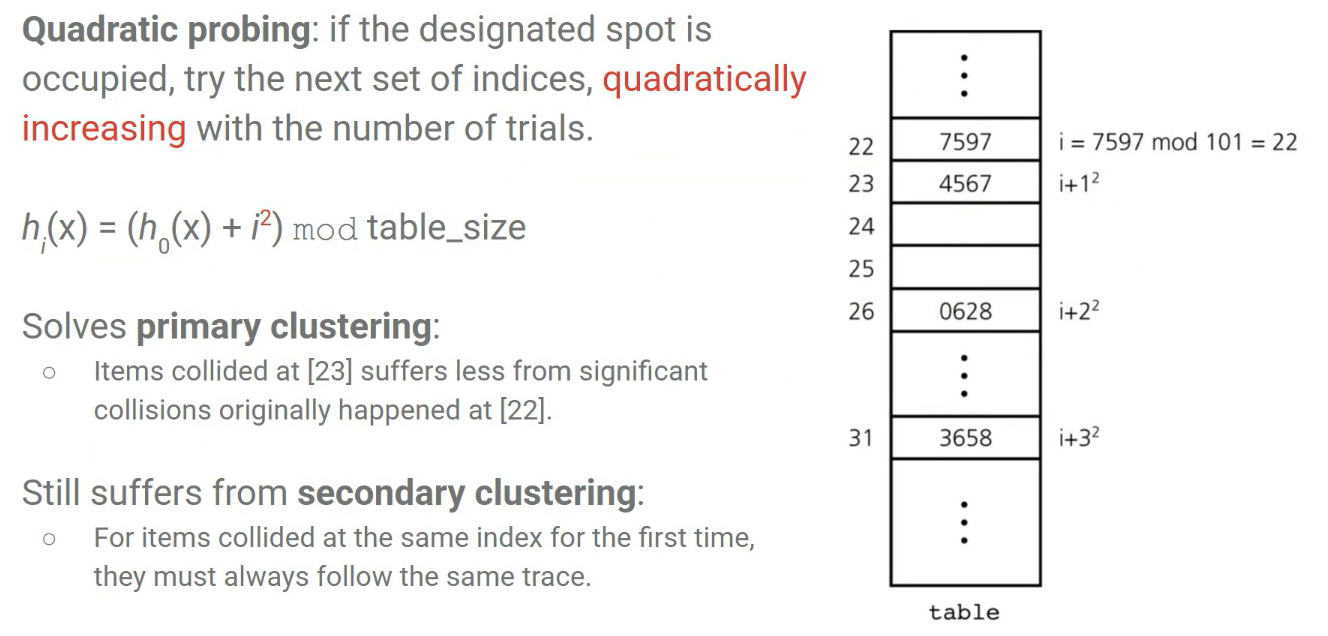

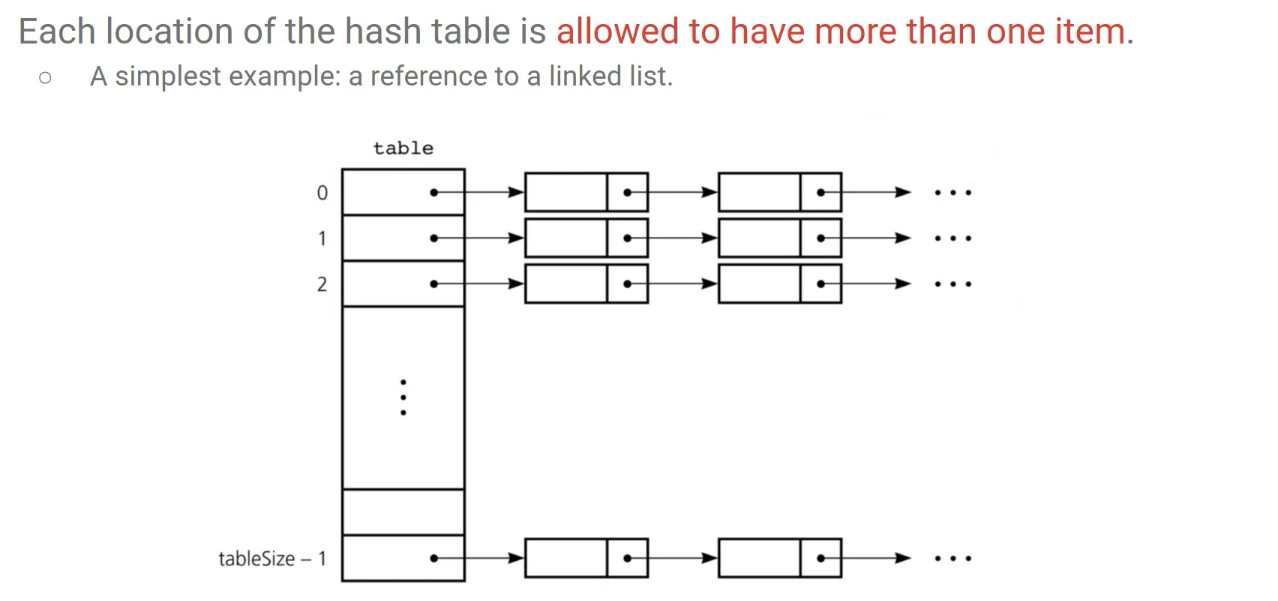
Separate Chaining
해시 테이블의 각 칸이 여러 개 원소를 담을 수 있도록 만드는 방법이다. 인덱스에 연결 리스트/벡터를 달아두고, 같은 인덱스로 해시된 원소들을 그 연결 리스트에 모아둔다. 반드시 연결 리스트일 필요는 없고, Tree/Vector 등 다른 ADT 구조를 사용할 수 있다.
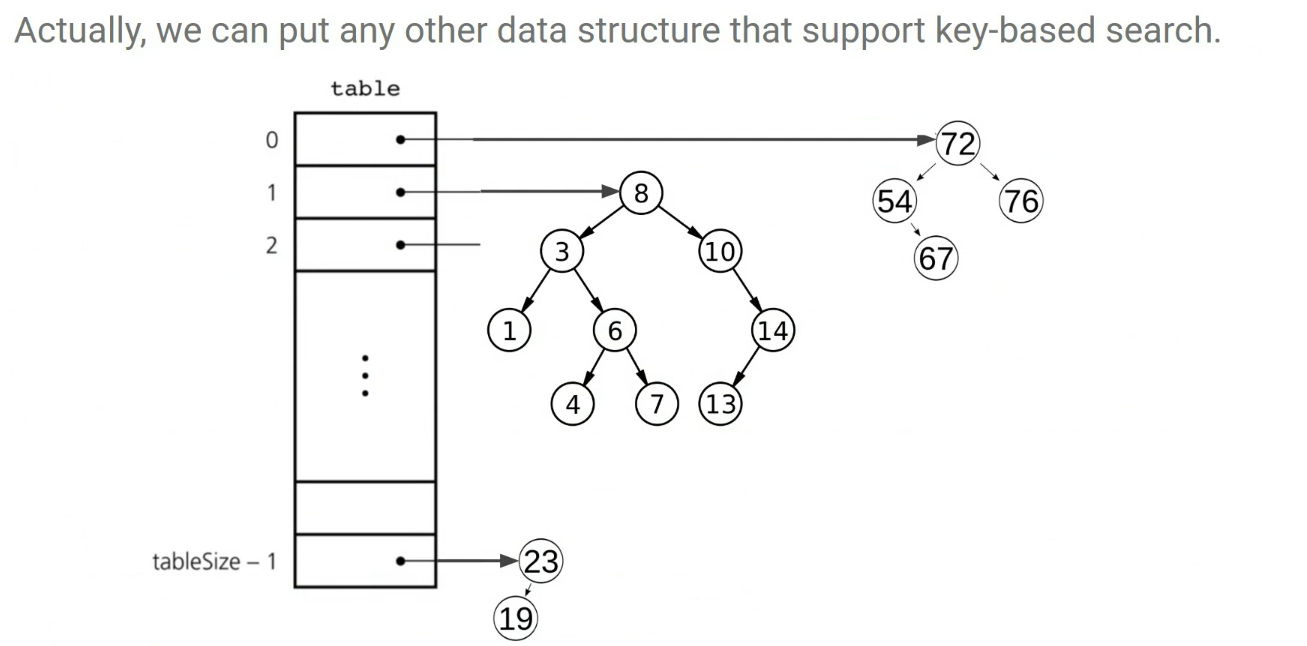
Performance of a Hash Table
해시 테이블의 성능은 원소 개수 그 자체보다 load factor α에 의해 결정된다.
load factor α = N/M
- N: 실제로 들어있는 원소 수
- M: 테이블 칸 수
- α가 커질수록 한 칸에 몰리는 평균 원소 수가 늘어나므로 느려진다.
Open addressing에서는 각 칸에 원소 1개만 들어가므로, α = 1이면 모든 칸이 꽉 차서 더 이상 삽입이 불가능하다. 따라서 α는 0~1 사이의 값을 항상 유지하고, α가 1에 가까워질수록 빈 칸을 찾기 위해 probe를 많이 하게 되어 시간이 급격히 증가한다.
Separate cahining에서는 각 칸이 여러 원소를 가질 수 있다. 따라서 α가 1보다 더 커질수가 있다.

Efficiency of Hashing
open addresing은 실패 탐색의 경우 빈 칸을 만날 때까지 계속 probe해야 해서 α가 커질수록 성능이 크게 감소하게 된다. Linear probing 방법은 primary clustering (한 곳에 뭉치는 현상) 때문에 연속 구간이 길게 생기고, 그 구간을 또 더 키우는 악순환이 생긴다. 따라서 α가 0.7~0.9만 돼도 급격하게 성능이 감소한다.
정리하면 α가 낮으면 어떤 방식이든 대체로 O(1)이 된다. 하지만 α가 커지면 open addresing은 특히 급격히 느려지고, chaining은 비교적 완만하게 느려진다. 따라서 실무에서는 α가 커지기 전에 reszie + rehash로 α를 지속적으로 낮게 유지한다.

How to Decide the Table Size (M)
해시 테이블 크기는 load factor (적재율) α = N / M를 원하는 수준으로 유지하도록 정하면 된다. 보통 α ≈ 0.6~0.75 정도가 속도/메모리 균형이 좋다고 알려져 있다.
또한 키에 주기/패턴이 있을 때 M이 100, 1000 같은 수면 특정 나머지에 몰릴 수 있으므로 101 / 1001 같은 소수를 사용하는 것이 효율적이다.
만약 데이터 크기가 어느정도인지 모르는 경우에는 적당한 테이블 크기로 시작하고, 삽입할 때마다 load factor를 계산해서 threshold보다 넘으면 resize + rehash를 진행한다. 새 테이블 크기는 보통 2배 정도로 잡고, 기존 원소들을 새 테이블 크기 기준으로 전부 다시 해시 계산해서 옮긴다.

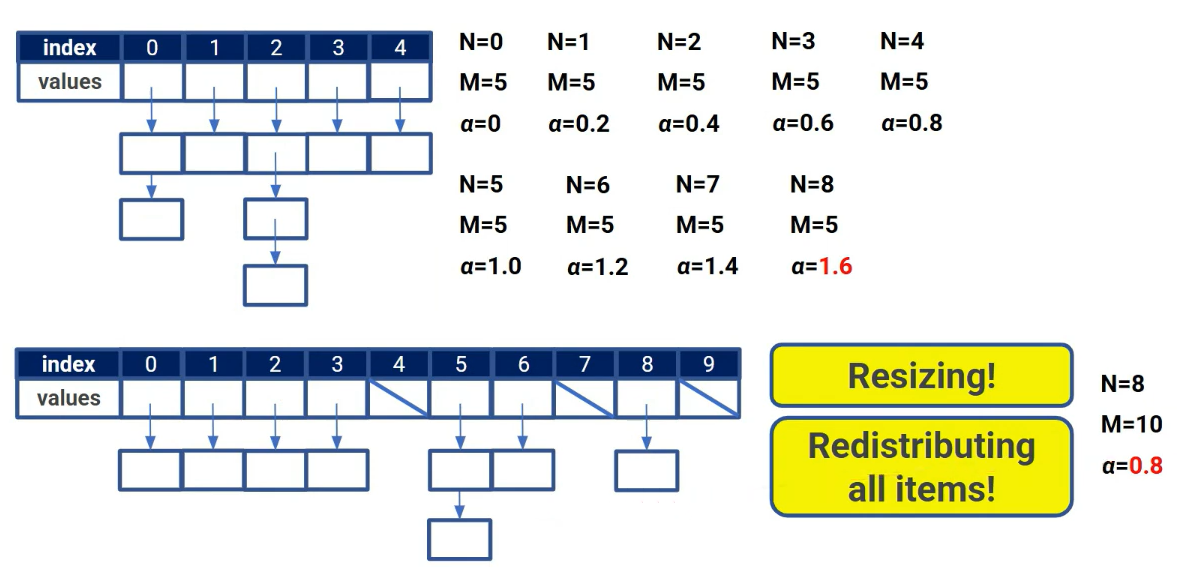
resize는 한 번 할 때마다 원소 N개를 재배치 해야하므로 O(N)의 시간이 걸린다. 하지만 자주 일어나지 않게 설계하므로 전체 삽입 N번 동안 재배치 비용이 평균적으로 O(1)로 계산된다.

3. Applications of Hash Tables




'2. Artificial Intelligence > Seoul National Univ. Data Science' 카테고리의 다른 글
| [Seoul National Univ: Data Science] Lecture 7. Graphs (0) | 2025.12.11 |
|---|---|
| [Seoul National Univ: Data Science] Lecture 6. Trees (1) | 2025.12.10 |
| [Seoul National Univ: Data Science] Lecture 5. Stacks & Queues (0) | 2025.12.08 |
| [Seoul National Univ: Data Science] Lecture 4. Arrays & Linked Lists (0) | 2025.12.07 |
| [Seoul National Univ: Data Science] Lecture 3. Sorting (0) | 2025.12.06 |





