2. Artificial Intelligence/Stanford Univ. CS231n
[Stanford Univ: CS231n] Spring 2025 Assignment1. Q3(Two-Layer Neural Network)
뉴하늘
2025. 4. 27. 20:56
728x90
본 포스팅은 Stanford University School of Engineering의 CS231n: Convolutional Neural Networks for Visual Recognition을 수강하고 공부한 내용을 정리하기 위한 포스팅입니다.
https://github.com/cs231n/cs231n.github.io/blob/master/assignments/2025/assignment1.md
cs231n.github.io/assignments/2025/assignment1.md at master · cs231n/cs231n.github.io
Public facing notes page. Contribute to cs231n/cs231n.github.io development by creating an account on GitHub.
github.com
https://github.com/KwonKiHyeok/cs231n
GitHub - KwonKiHyeok/CS231n: cs231n assignments
cs231n assignments. Contribute to KwonKiHyeok/CS231n development by creating an account on GitHub.
github.com
Q3: Two-Layer Neural Network
Affine Layer


def affine_forward(x, w, b):
"""
Computes the forward pass for an affine (fully-connected) layer.
The input x has shape (N, d_1, ..., d_k) and contains a minibatch of N
examples, where each example x[i] has shape (d_1, ..., d_k). We will
reshape each input into a vector of dimension D = d_1 * ... * d_k, and
then transform it to an output vector of dimension M.
Inputs:
- x: A numpy array containing input data, of shape (N, d_1, ..., d_k)
- w: A numpy array of weights, of shape (D, M)
- b: A numpy array of biases, of shape (M,)
Returns a tuple of:
- out: output, of shape (N, M)
- cache: (x, w, b)
"""
out = None
shape = x.shape
x = x.reshape(shape[0], -1)
out = x.dot(w) + b
x = x.reshape(shape)
cache = (x, w, b)
return out, cache
def affine_backward(dout, cache):
"""
Computes the backward pass for an affine layer.
Inputs:
- dout: Upstream derivative, of shape (N, M)
- cache: Tuple of:
- x: Input data, of shape (N, d_1, ... d_k)
- w: Weights, of shape (D, M)
- b: Biases, of shape (M,)
Returns a tuple of:
- dx: Gradient with respect to x, of shape (N, d1, ..., d_k)
- dw: Gradient with respect to w, of shape (D, M)
- db: Gradient with respect to b, of shape (M,)
"""
x, w, b = cache
dx, dw, db = None, None, None
shape = x.shape
dx = dout.dot(w.T).reshape(shape)
dw = x.reshape(shape[0], -1).T.dot(dout)
db = dout.sum(axis = 0)
return dx, dw, db
ReLU Function


def relu_forward(x):
"""
Computes the forward pass for a layer of rectified linear units (ReLUs).
Input:
- x: Inputs, of any shape
Returns a tuple of:
- out: Output, of the same shape as x
- cache: x
"""
out = None
out = np.maximum(0, x)
cache = x
return out, cache
def relu_backward(dout, cache):
"""
Computes the backward pass for a layer of rectified linear units (ReLUs).
Input:
- dout: Upstream derivatives, of any shape
- cache: Input x, of same shape as dout
Returns:
- dx: Gradient with respect to x
"""
dx, x = None, cache
dx = dout * (x > 0)
return dx

Loss Layers: Softmax

def softmax_loss(x, y):
"""
Computes the loss and gradient for softmax classification.
Inputs:
- x: Input data, of shape (N, C) where x[i, j] is the score for the jth
class for the ith input.
- y: Vector of labels, of shape (N,) where y[i] is the label for x[i] and
0 <= y[i] < C
Returns a tuple of:
- loss: Scalar giving the loss
- dx: Gradient of the loss with respect to x
"""
loss, dx = None, None
# Softmax Probabilities
p = np.exp(x - x.max(axis = 1, keepdims= True))
p /= p.sum(axis = 1, keepdims = True) # p shape = (N, C)
logp = np.log(p)
# Loss calculation
loss = -np.sum(logp[np.arange(x.shape[0]), y])
loss /= x.shape[0]
# Gradient calculation
p[range(x.shape[0]), y] -= 1
dx = p / x.shape[0]
return loss, dx

np.random.seed(231)
N, D, H, C = 3, 5, 50, 7
X = np.random.randn(N, D)
y = np.random.randint(C, size=N)
std = 1e-3
model = TwoLayerNet(input_dim=D, hidden_dim=H, num_classes=C, weight_scale=std)
print('Testing initialization ... ')
W1_std = abs(model.params['W1'].std() - std)
b1 = model.params['b1']
W2_std = abs(model.params['W2'].std() - std)
b2 = model.params['b2']
assert W1_std < std / 10, 'First layer weights do not seem right'
assert np.all(b1 == 0), 'First layer biases do not seem right'
assert W2_std < std / 10, 'Second layer weights do not seem right'
assert np.all(b2 == 0), 'Second layer biases do not seem right'
print('Testing test-time forward pass ... ')
model.params['W1'] = np.linspace(-0.7, 0.3, num=D*H).reshape(D, H)
model.params['b1'] = np.linspace(-0.1, 0.9, num=H)
model.params['W2'] = np.linspace(-0.3, 0.4, num=H*C).reshape(H, C)
model.params['b2'] = np.linspace(-0.9, 0.1, num=C)
X = np.linspace(-5.5, 4.5, num=N*D).reshape(D, N).T
scores = model.loss(X)
correct_scores = np.asarray(
[[11.53165108, 12.2917344, 13.05181771, 13.81190102, 14.57198434, 15.33206765, 16.09215096],
[12.05769098, 12.74614105, 13.43459113, 14.1230412, 14.81149128, 15.49994135, 16.18839143],
[12.58373087, 13.20054771, 13.81736455, 14.43418138, 15.05099822, 15.66781506, 16.2846319 ]])
scores_diff = np.abs(scores - correct_scores).sum()
assert scores_diff < 1e-6, 'Problem with test-time forward pass'
print('Testing training loss (no regularization)')
y = np.asarray([0, 5, 1])
loss, grads = model.loss(X, y)
correct_loss = 3.4702243556
assert abs(loss - correct_loss) < 1e-10, 'Problem with training-time loss'
model.reg = 1.0
loss, grads = model.loss(X, y)
correct_loss = 26.5948426952
assert abs(loss - correct_loss) < 1e-10, 'Problem with regularization loss'
# Errors should be around e-7 or less
for reg in [0.0, 0.7]:
print('Running numeric gradient check with reg = ', reg)
model.reg = reg
loss, grads = model.loss(X, y)
for name in sorted(grads):
f = lambda _: model.loss(X, y)[0]
grad_num = eval_numerical_gradient(f, model.params[name], verbose=False)
print('%s relative error: %.2e' % (name, rel_error(grad_num, grads[name])))
class TwoLayerNet(object):
"""
A two-layer fully-connected neural network with ReLU nonlinearity and
softmax loss that uses a modular layer design. We assume an input dimension
of D, a hidden dimension of H, and perform classification over C classes.
The architecure should be affine - relu - affine - softmax.
Note that this class does not implement gradient descent; instead, it
will interact with a separate Solver object that is responsible for running
optimization.
The learnable parameters of the model are stored in the dictionary
self.params that maps parameter names to numpy arrays.
"""
def __init__(
self,
input_dim=3 * 32 * 32,
hidden_dim=100,
num_classes=10,
weight_scale=1e-3,
reg=0.0,
):
"""
Initialize a new network.
Inputs:
- input_dim: An integer giving the size of the input
- hidden_dim: An integer giving the size of the hidden layer
- num_classes: An integer giving the number of classes to classify
- weight_scale: Scalar giving the standard deviation for random
initialization of the weights.
- reg: Scalar giving L2 regularization strength.
"""
self.params = {}
self.reg = reg
self.params['W1'] = weight_scale * np.random.randn(input_dim, hidden_dim)
self.params['b1'] = np.zeros(hidden_dim)
self.params['W2'] = weight_scale * np.random.randn(hidden_dim, num_classes)
self.params['b2'] = np.zeros(num_classes)
def loss(self, X, y=None):
"""
Compute loss and gradient for a minibatch of data.
Inputs:
- X: Array of input data of shape (N, d_1, ..., d_k)
- y: Array of labels, of shape (N,). y[i] gives the label for X[i].
Returns:
If y is None, then run a test-time forward pass of the model and return:
- scores: Array of shape (N, C) giving classification scores, where
scores[i, c] is the classification score for X[i] and class c.
If y is not None, then run a training-time forward and backward pass and
return a tuple of:
- loss: Scalar value giving the loss
- grads: Dictionary with the same keys as self.params, mapping parameter
names to gradients of the loss with respect to those parameters.
"""
scores = None
w1, b1 = self.params['W1'], self.params['b1']
w2, b2 = self.params['W2'], self.params['b2']
out1, cache1 = affine_forward(X, w1, b1)
out2, cache2 = relu_forward(out1)
scores, cache3 = affine_forward(out2, w2, b2)
# If y is None then we are in test mode so just return scores
if y is None:
return scores
loss, grads = 0, {}
loss, dloss = softmax_loss(scores, y)
loss += 0.5 * self.reg * (np.sum(w1 * w1) + np.sum(w2 * w2))
dout3, dw2, db2 = affine_backward(dloss, cache3)
dout2 = relu_backward(dout3, cache2)
dout1, dw1, db1 = affine_backward(dout2, cache1)
dw1 += self.reg * w1
dw2 += self.reg * w2
grads = {
'W1': dw1, 'W2': dw2, 'b1': db1, 'b2': db2
}
return loss, grads

input_size = 32 * 32 * 3
hidden_size = 50
num_classes = 10
model = TwoLayerNet(input_size, hidden_size, num_classes)
solver = None
##############################################################################
# TODO: Use a Solver instance to train a TwoLayerNet that achieves about 36% #
# accuracy on the validation set. #
##############################################################################
solver = Solver(model, data, optim_config = {'learning_rate': 1e-3})
solver.train()
##############################################################################
# END OF YOUR CODE #
##############################################################################(Iteration 1 / 4900) loss: 2.303340
(Epoch 0 / 10) train acc: 0.151000; val_acc: 0.139000
(Iteration 11 / 4900) loss: 2.271071
(Iteration 21 / 4900) loss: 2.167656
(Iteration 31 / 4900) loss: 2.108339
(Iteration 41 / 4900) loss: 1.976631
(Iteration 51 / 4900) loss: 1.951373
(Iteration 61 / 4900) loss: 2.086970
(Iteration 71 / 4900) loss: 1.868148
(Iteration 81 / 4900) loss: 1.913472
(Iteration 91 / 4900) loss: 1.775790
(Iteration 101 / 4900) loss: 1.867569
(Iteration 111 / 4900) loss: 1.889527
(Iteration 121 / 4900) loss: 1.913567
(Iteration 131 / 4900) loss: 1.760706
(Iteration 141 / 4900) loss: 1.785719
(Iteration 151 / 4900) loss: 1.820857
(Iteration 161 / 4900) loss: 1.608371
(Iteration 171 / 4900) loss: 1.808199
(Iteration 181 / 4900) loss: 1.633832
(Iteration 191 / 4900) loss: 1.790768
(Iteration 201 / 4900) loss: 1.710240
(Iteration 211 / 4900) loss: 1.742760
(Iteration 221 / 4900) loss: 1.576107
(Iteration 231 / 4900) loss: 1.697288
(Iteration 241 / 4900) loss: 1.552204
(Iteration 251 / 4900) loss: 1.688581
(Iteration 261 / 4900) loss: 1.812839
(Iteration 271 / 4900) loss: 1.605471
(Iteration 281 / 4900) loss: 1.608326
(Iteration 291 / 4900) loss: 1.651511
(Iteration 301 / 4900) loss: 1.725494
(Iteration 311 / 4900) loss: 1.681246
(Iteration 321 / 4900) loss: 1.502084
(Iteration 331 / 4900) loss: 1.623061
(Iteration 341 / 4900) loss: 1.544125
(Iteration 351 / 4900) loss: 1.601977
(Iteration 361 / 4900) loss: 1.819652
(Iteration 371 / 4900) loss: 1.543442
(Iteration 381 / 4900) loss: 1.677521
(Iteration 391 / 4900) loss: 1.415165
(Iteration 401 / 4900) loss: 1.767461
(Iteration 411 / 4900) loss: 1.627466
(Iteration 421 / 4900) loss: 1.582891
(Iteration 431 / 4900) loss: 1.484842
(Iteration 441 / 4900) loss: 1.618979
(Iteration 451 / 4900) loss: 1.587562
(Iteration 461 / 4900) loss: 1.719719
(Iteration 471 / 4900) loss: 1.553009
(Iteration 481 / 4900) loss: 1.743801
(Epoch 1 / 10) train acc: 0.427000; val_acc: 0.446000
(Iteration 491 / 4900) loss: 1.564622
(Iteration 501 / 4900) loss: 1.434767
(Iteration 511 / 4900) loss: 1.671771
(Iteration 521 / 4900) loss: 1.737396
(Iteration 531 / 4900) loss: 1.548779
(Iteration 541 / 4900) loss: 1.429637
(Iteration 551 / 4900) loss: 1.715906
(Iteration 561 / 4900) loss: 1.508951
(Iteration 571 / 4900) loss: 1.615843
(Iteration 581 / 4900) loss: 1.515214
(Iteration 591 / 4900) loss: 1.389328
(Iteration 601 / 4900) loss: 1.616783
(Iteration 611 / 4900) loss: 1.486592
(Iteration 621 / 4900) loss: 1.487262
(Iteration 631 / 4900) loss: 1.585451
(Iteration 641 / 4900) loss: 1.444013
(Iteration 651 / 4900) loss: 1.644154
(Iteration 661 / 4900) loss: 1.611669
(Iteration 671 / 4900) loss: 1.543733
(Iteration 681 / 4900) loss: 1.610559
(Iteration 691 / 4900) loss: 1.547267
(Iteration 701 / 4900) loss: 1.591634
(Iteration 711 / 4900) loss: 1.639233
(Iteration 721 / 4900) loss: 1.520389
(Iteration 731 / 4900) loss: 1.487215
(Iteration 741 / 4900) loss: 1.418386
(Iteration 751 / 4900) loss: 1.678821
(Iteration 761 / 4900) loss: 1.686959
(Iteration 771 / 4900) loss: 1.669708
(Iteration 781 / 4900) loss: 1.789214
(Iteration 791 / 4900) loss: 1.516285
(Iteration 801 / 4900) loss: 1.856580
(Iteration 811 / 4900) loss: 1.737919
(Iteration 821 / 4900) loss: 1.589123
(Iteration 831 / 4900) loss: 1.448118
(Iteration 841 / 4900) loss: 1.421576
(Iteration 851 / 4900) loss: 1.453231
(Iteration 861 / 4900) loss: 1.557944
(Iteration 871 / 4900) loss: 1.631740
(Iteration 881 / 4900) loss: 1.672753
(Iteration 891 / 4900) loss: 1.585880
(Iteration 901 / 4900) loss: 1.393467
(Iteration 911 / 4900) loss: 1.709376
(Iteration 921 / 4900) loss: 1.519179
(Iteration 931 / 4900) loss: 1.490380
(Iteration 941 / 4900) loss: 1.481047
(Iteration 951 / 4900) loss: 1.537324
(Iteration 961 / 4900) loss: 1.494506
(Iteration 971 / 4900) loss: 1.405351
(Epoch 2 / 10) train acc: 0.477000; val_acc: 0.422000
(Iteration 981 / 4900) loss: 1.518194
(Iteration 991 / 4900) loss: 1.756746
(Iteration 1001 / 4900) loss: 1.448194
(Iteration 1011 / 4900) loss: 1.539389
(Iteration 1021 / 4900) loss: 1.494210
(Iteration 1031 / 4900) loss: 1.651692
(Iteration 1041 / 4900) loss: 1.510391
(Iteration 1051 / 4900) loss: 1.394123
(Iteration 1061 / 4900) loss: 1.523633
(Iteration 1071 / 4900) loss: 1.681147
(Iteration 1081 / 4900) loss: 1.366720
(Iteration 1091 / 4900) loss: 1.401193
(Iteration 1101 / 4900) loss: 1.489001
(Iteration 1111 / 4900) loss: 1.532704
(Iteration 1121 / 4900) loss: 1.394761
(Iteration 1131 / 4900) loss: 1.772122
(Iteration 1141 / 4900) loss: 1.460733
(Iteration 1151 / 4900) loss: 1.437895
(Iteration 1161 / 4900) loss: 1.474207
(Iteration 1171 / 4900) loss: 1.358036
(Iteration 1181 / 4900) loss: 1.438127
(Iteration 1191 / 4900) loss: 1.451817
(Iteration 1201 / 4900) loss: 1.448320
(Iteration 1211 / 4900) loss: 1.443717
(Iteration 1221 / 4900) loss: 1.554821
(Iteration 1231 / 4900) loss: 1.539013
(Iteration 1241 / 4900) loss: 1.371532
(Iteration 1251 / 4900) loss: 1.609694
(Iteration 1261 / 4900) loss: 1.408299
(Iteration 1271 / 4900) loss: 1.399595
(Iteration 1281 / 4900) loss: 1.404865
(Iteration 1291 / 4900) loss: 1.504542
(Iteration 1301 / 4900) loss: 1.384340
(Iteration 1311 / 4900) loss: 1.266890
(Iteration 1321 / 4900) loss: 1.291466
(Iteration 1331 / 4900) loss: 1.498872
(Iteration 1341 / 4900) loss: 1.594052
(Iteration 1351 / 4900) loss: 1.618512
(Iteration 1361 / 4900) loss: 1.368880
(Iteration 1371 / 4900) loss: 1.495235
(Iteration 1381 / 4900) loss: 1.345083
(Iteration 1391 / 4900) loss: 1.413414
(Iteration 1401 / 4900) loss: 1.625223
(Iteration 1411 / 4900) loss: 1.595104
(Iteration 1421 / 4900) loss: 1.359285
(Iteration 1431 / 4900) loss: 1.412155
(Iteration 1441 / 4900) loss: 1.414258
(Iteration 1451 / 4900) loss: 1.618599
(Iteration 1461 / 4900) loss: 1.593964
(Epoch 3 / 10) train acc: 0.479000; val_acc: 0.466000
(Iteration 1471 / 4900) loss: 1.282962
(Iteration 1481 / 4900) loss: 1.387572
(Iteration 1491 / 4900) loss: 1.411815
(Iteration 1501 / 4900) loss: 1.453267
(Iteration 1511 / 4900) loss: 1.493315
(Iteration 1521 / 4900) loss: 1.548238
(Iteration 1531 / 4900) loss: 1.508109
(Iteration 1541 / 4900) loss: 1.473534
(Iteration 1551 / 4900) loss: 1.285852
(Iteration 1561 / 4900) loss: 1.326537
(Iteration 1571 / 4900) loss: 1.741425
(Iteration 1581 / 4900) loss: 1.426781
(Iteration 1591 / 4900) loss: 1.362742
(Iteration 1601 / 4900) loss: 1.401670
(Iteration 1611 / 4900) loss: 1.597393
(Iteration 1621 / 4900) loss: 1.324426
(Iteration 1631 / 4900) loss: 1.435459
(Iteration 1641 / 4900) loss: 1.122484
(Iteration 1651 / 4900) loss: 1.460434
(Iteration 1661 / 4900) loss: 1.504328
(Iteration 1671 / 4900) loss: 1.462337
(Iteration 1681 / 4900) loss: 1.413372
(Iteration 1691 / 4900) loss: 1.155611
(Iteration 1701 / 4900) loss: 1.482391
(Iteration 1711 / 4900) loss: 1.442646
(Iteration 1721 / 4900) loss: 1.537932
(Iteration 1731 / 4900) loss: 1.522875
(Iteration 1741 / 4900) loss: 1.323501
(Iteration 1751 / 4900) loss: 1.419302
(Iteration 1761 / 4900) loss: 1.422297
(Iteration 1771 / 4900) loss: 1.365183
(Iteration 1781 / 4900) loss: 1.626447
(Iteration 1791 / 4900) loss: 1.410908
(Iteration 1801 / 4900) loss: 1.161634
(Iteration 1811 / 4900) loss: 1.507683
(Iteration 1821 / 4900) loss: 1.267325
(Iteration 1831 / 4900) loss: 1.633199
(Iteration 1841 / 4900) loss: 1.273187
(Iteration 1851 / 4900) loss: 1.468949
(Iteration 1861 / 4900) loss: 1.301038
(Iteration 1871 / 4900) loss: 1.285429
(Iteration 1881 / 4900) loss: 1.357060
(Iteration 1891 / 4900) loss: 1.379960
(Iteration 1901 / 4900) loss: 1.556033
(Iteration 1911 / 4900) loss: 1.573812
(Iteration 1921 / 4900) loss: 1.304783
(Iteration 1931 / 4900) loss: 1.275486
(Iteration 1941 / 4900) loss: 1.473024
(Iteration 1951 / 4900) loss: 1.573940
(Epoch 4 / 10) train acc: 0.516000; val_acc: 0.463000
(Iteration 1961 / 4900) loss: 1.593102
(Iteration 1971 / 4900) loss: 1.376981
(Iteration 1981 / 4900) loss: 1.510240
(Iteration 1991 / 4900) loss: 1.489145
(Iteration 2001 / 4900) loss: 1.438528
(Iteration 2011 / 4900) loss: 1.409874
(Iteration 2021 / 4900) loss: 1.438425
(Iteration 2031 / 4900) loss: 1.336733
(Iteration 2041 / 4900) loss: 1.493979
(Iteration 2051 / 4900) loss: 1.266203
(Iteration 2061 / 4900) loss: 1.763093
(Iteration 2071 / 4900) loss: 1.363556
(Iteration 2081 / 4900) loss: 1.459880
(Iteration 2091 / 4900) loss: 1.307505
(Iteration 2101 / 4900) loss: 1.694364
(Iteration 2111 / 4900) loss: 1.333825
(Iteration 2121 / 4900) loss: 1.244581
(Iteration 2131 / 4900) loss: 1.419890
(Iteration 2141 / 4900) loss: 1.426067
(Iteration 2151 / 4900) loss: 1.467463
(Iteration 2161 / 4900) loss: 1.630520
(Iteration 2171 / 4900) loss: 1.575261
(Iteration 2181 / 4900) loss: 1.482760
(Iteration 2191 / 4900) loss: 1.213142
(Iteration 2201 / 4900) loss: 1.345261
(Iteration 2211 / 4900) loss: 1.602117
(Iteration 2221 / 4900) loss: 1.574083
(Iteration 2231 / 4900) loss: 1.197135
(Iteration 2241 / 4900) loss: 1.358047
(Iteration 2251 / 4900) loss: 1.215567
(Iteration 2261 / 4900) loss: 1.227838
(Iteration 2271 / 4900) loss: 1.393001
(Iteration 2281 / 4900) loss: 1.332190
(Iteration 2291 / 4900) loss: 1.403928
(Iteration 2301 / 4900) loss: 1.244864
(Iteration 2311 / 4900) loss: 1.264825
(Iteration 2321 / 4900) loss: 1.370733
(Iteration 2331 / 4900) loss: 1.295206
(Iteration 2341 / 4900) loss: 1.614658
(Iteration 2351 / 4900) loss: 1.423703
(Iteration 2361 / 4900) loss: 1.432278
(Iteration 2371 / 4900) loss: 1.239919
(Iteration 2381 / 4900) loss: 1.451798
(Iteration 2391 / 4900) loss: 1.441152
(Iteration 2401 / 4900) loss: 1.304167
(Iteration 2411 / 4900) loss: 1.427407
(Iteration 2421 / 4900) loss: 1.511304
(Iteration 2431 / 4900) loss: 1.621086
(Iteration 2441 / 4900) loss: 1.400170
(Epoch 5 / 10) train acc: 0.519000; val_acc: 0.481000
(Iteration 2451 / 4900) loss: 1.464522
(Iteration 2461 / 4900) loss: 1.499452
(Iteration 2471 / 4900) loss: 1.448497
(Iteration 2481 / 4900) loss: 1.200939
(Iteration 2491 / 4900) loss: 1.391180
(Iteration 2501 / 4900) loss: 1.196326
(Iteration 2511 / 4900) loss: 1.328154
(Iteration 2521 / 4900) loss: 1.321794
(Iteration 2531 / 4900) loss: 1.311650
(Iteration 2541 / 4900) loss: 1.334811
(Iteration 2551 / 4900) loss: 1.719133
(Iteration 2561 / 4900) loss: 1.283756
(Iteration 2571 / 4900) loss: 1.551682
(Iteration 2581 / 4900) loss: 1.357318
(Iteration 2591 / 4900) loss: 1.414364
(Iteration 2601 / 4900) loss: 1.434822
(Iteration 2611 / 4900) loss: 1.349276
(Iteration 2621 / 4900) loss: 1.292765
(Iteration 2631 / 4900) loss: 1.307457
(Iteration 2641 / 4900) loss: 1.300684
(Iteration 2651 / 4900) loss: 1.280672
(Iteration 2661 / 4900) loss: 1.378231
(Iteration 2671 / 4900) loss: 1.197038
(Iteration 2681 / 4900) loss: 1.348350
(Iteration 2691 / 4900) loss: 1.495787
(Iteration 2701 / 4900) loss: 1.536024
(Iteration 2711 / 4900) loss: 1.439203
(Iteration 2721 / 4900) loss: 1.294962
(Iteration 2731 / 4900) loss: 1.379765
(Iteration 2741 / 4900) loss: 1.435709
(Iteration 2751 / 4900) loss: 1.315105
(Iteration 2761 / 4900) loss: 1.415999
(Iteration 2771 / 4900) loss: 1.421049
(Iteration 2781 / 4900) loss: 1.169496
(Iteration 2791 / 4900) loss: 1.221156
(Iteration 2801 / 4900) loss: 1.600799
(Iteration 2811 / 4900) loss: 1.553342
(Iteration 2821 / 4900) loss: 1.327634
(Iteration 2831 / 4900) loss: 1.485586
(Iteration 2841 / 4900) loss: 1.439970
(Iteration 2851 / 4900) loss: 1.369139
(Iteration 2861 / 4900) loss: 1.288424
(Iteration 2871 / 4900) loss: 1.609286
(Iteration 2881 / 4900) loss: 1.482526
(Iteration 2891 / 4900) loss: 1.256474
(Iteration 2901 / 4900) loss: 1.722736
(Iteration 2911 / 4900) loss: 1.387079
(Iteration 2921 / 4900) loss: 1.198407
(Iteration 2931 / 4900) loss: 1.378056
(Epoch 6 / 10) train acc: 0.551000; val_acc: 0.503000
(Iteration 2941 / 4900) loss: 1.387689
(Iteration 2951 / 4900) loss: 1.329715
(Iteration 2961 / 4900) loss: 1.369628
(Iteration 2971 / 4900) loss: 1.104668
(Iteration 2981 / 4900) loss: 1.247975
(Iteration 2991 / 4900) loss: 1.398242
(Iteration 3001 / 4900) loss: 1.528935
(Iteration 3011 / 4900) loss: 1.361539
(Iteration 3021 / 4900) loss: 1.365478
(Iteration 3031 / 4900) loss: 1.284084
(Iteration 3041 / 4900) loss: 1.200773
(Iteration 3051 / 4900) loss: 1.355251
(Iteration 3061 / 4900) loss: 1.389494
(Iteration 3071 / 4900) loss: 1.409950
(Iteration 3081 / 4900) loss: 1.272530
(Iteration 3091 / 4900) loss: 1.453960
(Iteration 3101 / 4900) loss: 1.455121
(Iteration 3111 / 4900) loss: 1.301807
(Iteration 3121 / 4900) loss: 1.261802
(Iteration 3131 / 4900) loss: 1.072448
(Iteration 3141 / 4900) loss: 1.579569
(Iteration 3151 / 4900) loss: 1.350368
(Iteration 3161 / 4900) loss: 1.355613
(Iteration 3171 / 4900) loss: 1.315471
(Iteration 3181 / 4900) loss: 1.117946
(Iteration 3191 / 4900) loss: 1.426882
(Iteration 3201 / 4900) loss: 1.150338
(Iteration 3211 / 4900) loss: 1.542611
(Iteration 3221 / 4900) loss: 1.306920
(Iteration 3231 / 4900) loss: 1.483864
(Iteration 3241 / 4900) loss: 1.111939
(Iteration 3251 / 4900) loss: 1.314453
(Iteration 3261 / 4900) loss: 1.498091
(Iteration 3271 / 4900) loss: 1.303444
(Iteration 3281 / 4900) loss: 1.305542
(Iteration 3291 / 4900) loss: 1.515161
(Iteration 3301 / 4900) loss: 1.251608
(Iteration 3311 / 4900) loss: 1.512659
(Iteration 3321 / 4900) loss: 1.305299
(Iteration 3331 / 4900) loss: 1.498219
(Iteration 3341 / 4900) loss: 1.444276
(Iteration 3351 / 4900) loss: 1.377126
(Iteration 3361 / 4900) loss: 1.604155
(Iteration 3371 / 4900) loss: 1.232426
(Iteration 3381 / 4900) loss: 1.325397
(Iteration 3391 / 4900) loss: 1.612040
(Iteration 3401 / 4900) loss: 1.491525
(Iteration 3411 / 4900) loss: 1.403204
(Iteration 3421 / 4900) loss: 1.473107
(Epoch 7 / 10) train acc: 0.547000; val_acc: 0.485000
(Iteration 3431 / 4900) loss: 1.462015
(Iteration 3441 / 4900) loss: 1.078182
(Iteration 3451 / 4900) loss: 1.232023
(Iteration 3461 / 4900) loss: 1.256862
(Iteration 3471 / 4900) loss: 1.252942
(Iteration 3481 / 4900) loss: 1.432699
(Iteration 3491 / 4900) loss: 1.298057
(Iteration 3501 / 4900) loss: 1.259311
(Iteration 3511 / 4900) loss: 1.415653
(Iteration 3521 / 4900) loss: 1.270932
(Iteration 3531 / 4900) loss: 1.281123
(Iteration 3541 / 4900) loss: 1.653739
(Iteration 3551 / 4900) loss: 1.224265
(Iteration 3561 / 4900) loss: 1.377731
(Iteration 3571 / 4900) loss: 1.274362
(Iteration 3581 / 4900) loss: 1.177990
(Iteration 3591 / 4900) loss: 1.195414
(Iteration 3601 / 4900) loss: 1.306881
(Iteration 3611 / 4900) loss: 1.576095
(Iteration 3621 / 4900) loss: 1.164334
(Iteration 3631 / 4900) loss: 1.469397
(Iteration 3641 / 4900) loss: 1.135251
(Iteration 3651 / 4900) loss: 1.288501
(Iteration 3661 / 4900) loss: 1.359115
(Iteration 3671 / 4900) loss: 1.469039
(Iteration 3681 / 4900) loss: 1.306410
(Iteration 3691 / 4900) loss: 1.460180
(Iteration 3701 / 4900) loss: 1.359713
(Iteration 3711 / 4900) loss: 1.513890
(Iteration 3721 / 4900) loss: 1.449797
(Iteration 3731 / 4900) loss: 1.334646
(Iteration 3741 / 4900) loss: 1.285624
(Iteration 3751 / 4900) loss: 1.355996
(Iteration 3761 / 4900) loss: 1.228858
(Iteration 3771 / 4900) loss: 1.385221
(Iteration 3781 / 4900) loss: 1.198159
(Iteration 3791 / 4900) loss: 1.331873
(Iteration 3801 / 4900) loss: 1.381421
(Iteration 3811 / 4900) loss: 1.247329
(Iteration 3821 / 4900) loss: 1.161468
(Iteration 3831 / 4900) loss: 1.171269
(Iteration 3841 / 4900) loss: 1.515562
(Iteration 3851 / 4900) loss: 1.499166
(Iteration 3861 / 4900) loss: 1.303736
(Iteration 3871 / 4900) loss: 1.269355
(Iteration 3881 / 4900) loss: 1.157312
(Iteration 3891 / 4900) loss: 1.599091
(Iteration 3901 / 4900) loss: 1.181102
(Iteration 3911 / 4900) loss: 1.341982
(Epoch 8 / 10) train acc: 0.535000; val_acc: 0.480000
(Iteration 3921 / 4900) loss: 1.268377
(Iteration 3931 / 4900) loss: 1.220314
(Iteration 3941 / 4900) loss: 1.083533
(Iteration 3951 / 4900) loss: 1.382751
(Iteration 3961 / 4900) loss: 1.313230
(Iteration 3971 / 4900) loss: 1.460589
(Iteration 3981 / 4900) loss: 1.242050
(Iteration 3991 / 4900) loss: 1.568833
(Iteration 4001 / 4900) loss: 1.398056
(Iteration 4011 / 4900) loss: 1.308422
(Iteration 4021 / 4900) loss: 1.286550
(Iteration 4031 / 4900) loss: 1.184375
(Iteration 4041 / 4900) loss: 1.458917
(Iteration 4051 / 4900) loss: 1.311770
(Iteration 4061 / 4900) loss: 1.295118
(Iteration 4071 / 4900) loss: 1.393381
(Iteration 4081 / 4900) loss: 1.322092
(Iteration 4091 / 4900) loss: 1.308043
(Iteration 4101 / 4900) loss: 1.367847
(Iteration 4111 / 4900) loss: 1.440645
(Iteration 4121 / 4900) loss: 1.286069
(Iteration 4131 / 4900) loss: 1.309929
(Iteration 4141 / 4900) loss: 1.291994
(Iteration 4151 / 4900) loss: 1.323360
(Iteration 4161 / 4900) loss: 1.411986
(Iteration 4171 / 4900) loss: 1.218157
(Iteration 4181 / 4900) loss: 1.428425
(Iteration 4191 / 4900) loss: 1.187064
(Iteration 4201 / 4900) loss: 1.272496
(Iteration 4211 / 4900) loss: 1.392703
(Iteration 4221 / 4900) loss: 1.238428
(Iteration 4231 / 4900) loss: 1.335650
(Iteration 4241 / 4900) loss: 1.611871
(Iteration 4251 / 4900) loss: 1.461439
(Iteration 4261 / 4900) loss: 1.423267
(Iteration 4271 / 4900) loss: 1.273442
(Iteration 4281 / 4900) loss: 1.171634
(Iteration 4291 / 4900) loss: 1.197780
(Iteration 4301 / 4900) loss: 1.330841
(Iteration 4311 / 4900) loss: 1.211878
(Iteration 4321 / 4900) loss: 1.306080
(Iteration 4331 / 4900) loss: 1.314368
(Iteration 4341 / 4900) loss: 1.294477
(Iteration 4351 / 4900) loss: 1.358119
(Iteration 4361 / 4900) loss: 1.173900
(Iteration 4371 / 4900) loss: 1.342591
(Iteration 4381 / 4900) loss: 1.386023
(Iteration 4391 / 4900) loss: 1.387014
(Iteration 4401 / 4900) loss: 1.050800
(Epoch 9 / 10) train acc: 0.545000; val_acc: 0.473000
(Iteration 4411 / 4900) loss: 1.233973
(Iteration 4421 / 4900) loss: 1.516818
(Iteration 4431 / 4900) loss: 1.162969
(Iteration 4441 / 4900) loss: 1.530654
(Iteration 4451 / 4900) loss: 1.474264
(Iteration 4461 / 4900) loss: 1.334491
(Iteration 4471 / 4900) loss: 1.208461
(Iteration 4481 / 4900) loss: 1.430172
(Iteration 4491 / 4900) loss: 1.299060
(Iteration 4501 / 4900) loss: 1.264135
(Iteration 4511 / 4900) loss: 1.273518
(Iteration 4521 / 4900) loss: 1.269194
(Iteration 4531 / 4900) loss: 1.385419
(Iteration 4541 / 4900) loss: 1.486461
(Iteration 4551 / 4900) loss: 1.448231
(Iteration 4561 / 4900) loss: 1.483105
(Iteration 4571 / 4900) loss: 1.503206
(Iteration 4581 / 4900) loss: 1.313561
(Iteration 4591 / 4900) loss: 1.254811
(Iteration 4601 / 4900) loss: 1.399710
(Iteration 4611 / 4900) loss: 1.520757
(Iteration 4621 / 4900) loss: 1.181911
(Iteration 4631 / 4900) loss: 1.141000
(Iteration 4641 / 4900) loss: 1.430504
(Iteration 4651 / 4900) loss: 1.301318
(Iteration 4661 / 4900) loss: 1.354816
(Iteration 4671 / 4900) loss: 1.158177
(Iteration 4681 / 4900) loss: 1.279763
(Iteration 4691 / 4900) loss: 1.194458
(Iteration 4701 / 4900) loss: 1.426631
(Iteration 4711 / 4900) loss: 1.348481
(Iteration 4721 / 4900) loss: 1.289230
(Iteration 4731 / 4900) loss: 1.162886
(Iteration 4741 / 4900) loss: 1.237245
(Iteration 4751 / 4900) loss: 1.237935
(Iteration 4761 / 4900) loss: 1.257739
(Iteration 4771 / 4900) loss: 1.309592
(Iteration 4781 / 4900) loss: 1.204190
(Iteration 4791 / 4900) loss: 1.335356
(Iteration 4801 / 4900) loss: 1.074885
(Iteration 4811 / 4900) loss: 1.203644
(Iteration 4821 / 4900) loss: 1.152871
(Iteration 4831 / 4900) loss: 1.277136
(Iteration 4841 / 4900) loss: 1.263432
(Iteration 4851 / 4900) loss: 1.300143
(Iteration 4861 / 4900) loss: 1.353788
(Iteration 4871 / 4900) loss: 1.293113
(Iteration 4881 / 4900) loss: 1.246254
(Iteration 4891 / 4900) loss: 1.202679
(Epoch 10 / 10) train acc: 0.551000; val_acc: 0.482000

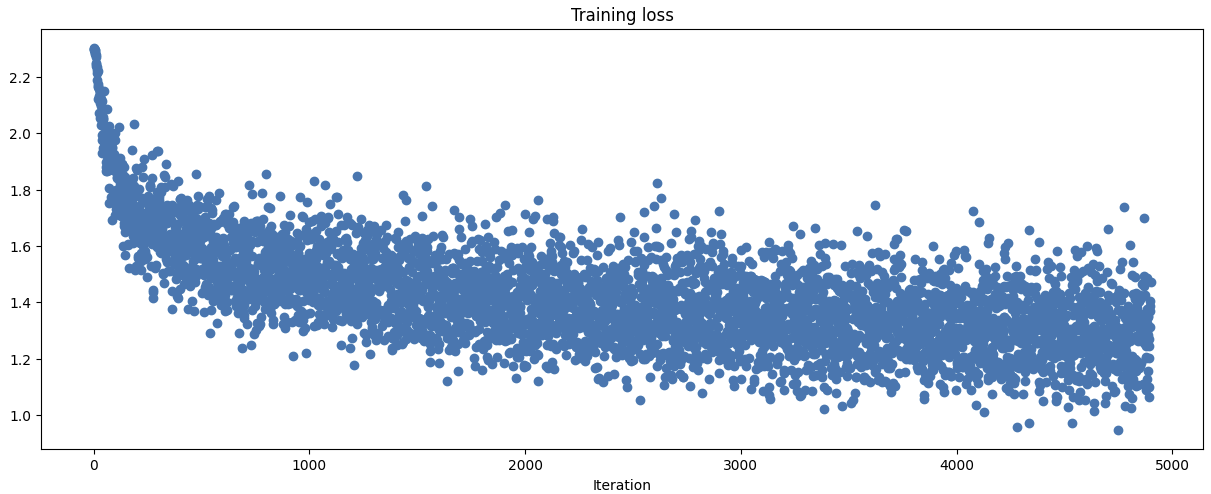




best_model = None
#################################################################################
# TODO: Tune hyperparameters using the validation set. Store your best trained #
# model in best_model. #
# #
# To help debug your network, it may help to use visualizations similar to the #
# ones we used above; these visualizations will have significant qualitative #
# differences from the ones we saw above for the poorly tuned network. #
# #
# Tweaking hyperparameters by hand can be fun, but you might find it useful to #
# write code to sweep through possible combinations of hyperparameters #
# automatically like we did on thexs previous exercises. #
#################################################################################
results = {}
best_val = -1
learning_rates = np.geomspace(3e-4, 3e-2, 3)
regularization_strengths = np.geomspace(1e-6, 1e-2, 5)
hidden_dim = np.array([64, 128, 256])
import itertools
for hidden in hidden_dim:
for lr, reg in itertools.product(learning_rates, regularization_strengths):
# Create Two Layer Net and train it with Solver
model = TwoLayerNet(hidden, reg=reg)
solver = Solver(model, data, optim_config={'learning_rate': lr}, num_epochs=10, verbose=False)
solver.train()
# Compute validation set accuracy and append to the dictionary
results[(hidden, lr, reg)] = solver.best_val_acc
# Save if validation accuracy is the best
if results[(hidden, lr, reg)] > best_val:
best_val = results[(hidden, lr, reg)]
best_model = model
# Print out results
for hidden, lr, reg in sorted(results):
val_accuracy = results[(hidden, lr, reg)]
print('hidden %e lr %e reg %e val accuracy: %f' % (hidden, lr, reg, val_accuracy))
print('best validation accuracy achieved during cross-validation: %f' % best_val)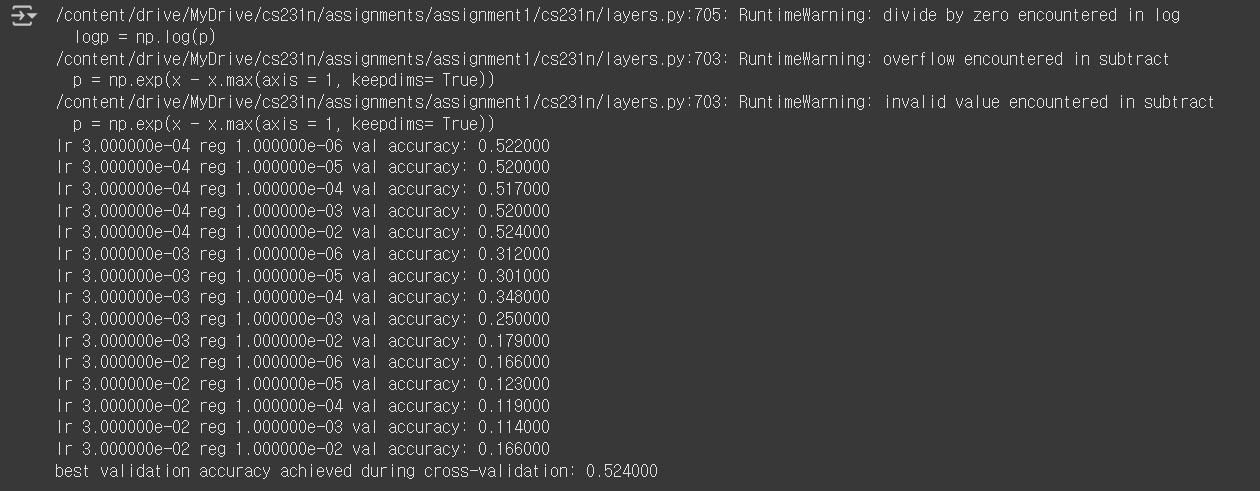

728x90
